This is an old revision of the document!
파운틴 코드
Fountain Codes
Random Binary Fountain Code
파운틴코드를 다루는 논문들에서 비교 대상이 되곤 하는 이상적 파운틴코드이다. 랜덤 바이너리 파운틴코드는 완전히 랜덤한 분포를 가진 매트릭스를 사용하여 인코딩심볼을 생성하는 것을 가정한다. 이 경우 가우스 소거법(Gaussian-Elimination; 이하 GE)을 사용하면 섀넌리밋에 근접하는 적은 전송 오버헤드로 디코딩 할 수 있지만 매트릭스의 밀도가 1/2에 달하여 GE 연산 오버헤드 측면에서 실용적이지 못한 문제가 있다.
Luby Transform Code
루비트랜스폼코드는 신뢰전파(Belief-Propagation; 이하 BP) 알고리즘을 사용한 디코딩이 가능하도록 인코딩 단계에서 솔리톤분포(Soliton-Distribution)를 사용하여 매트릭스 밀도를 낮춤으로써 최초의 실용적인 파운틴코드로 인정받을 수 있었다. BP는 심볼 수 K에 대해 유사선형복잡도에 해당하는 O(nlogn)으로 디코딩 가능하며, 솔리톤분포에 의해 생성되는 매트릭스의 밀도가 낮아 GE로 디코딩하는 경우에도 랜덤 바이너리 파운틴코드에 비해 빠르게 연산할 수 있다. 그러나 LT에서의 BP 디코딩은 충분한 K 값을 가져야 논문에서 제시하는 성능을 보이며, GE 디코딩의 경우 매트릭스 밀도가 너무 낮은 나머지 RANK 부족을 자주 겪는다. 솔리톤분포의 파라메터를 조절하여 매트릭스의 밀도를 상향하는 것이 가능하지만, 이 경우 끊임 없이 Degree 1 ( 무게 1 ) 심볼을 생성해야만 하는 BP 디코딩 알고리즘의 동작을 방해하게 되고, 이는 디코딩 성공확률의 편차를 크게 하여 전송 오버헤드의 예측이 어려워진다.
Raptor Code, R10, RQ
LT Code의 경우 BP와 GE 알고리즘을 혼합하여 디코딩하였을 때 좋은 결과를 보이는데, 이 하이브리드 디코딩 알고리즘의 최종 보스격인 것이 Raptor Code(이하 R10)논문에서 제시 된 Inactivation Decoding이다. 또한 랩터코드에서는 제약심볼이라 지칭하는 가상의 중간심볼을 생성하여 솔리톤분포를 크게 손상하지 않고 매트릭스의 밀도를 상향하였기에 충분한 RANK를 확보한다. RaptorQ(이하 RQ)의 경우 R10의 고밀도 매트릭스 영역을 0과 1의 바이너리가 아닌 0~255의 GF(28)로 대체하여 RANK 부족을 극적으로 억제하며 Permanent Inactivation Decoding이라 지칭하는 방법으로 BP 디코딩 동작에 영향을 주지 않도록 고밀도 매트릭스 영역을 숨긴다.
접근 순서
필자의 경우 수학에 익숙하지 않아 상당한 진입장벽을 경험하였는데, Raptor를 먼저 접하고 공부하다가 근간이 되는 Luby-Transform을 파고 들었고, 여기서 Belief-Propagation 알고리즘에 대한 이해를 얻어 LT코드에서의 BP-GE hybrid decoder를 연구하게 되었다. 이후 BP-GE hybrid decoder 연구를 완성시킬 즈음에서야 RFC-5053이 설명하고 있는 Inactivation-Decoding의 핵심을 이해하게 되면서 Raptor로 멀리 돌아온 케이스이다.
각 코드의 오리지널 논문은 인코딩 매트릭스 구성에 맞는 디코더를 함께 제안하고 있는데, 이를 파악하는 것이 최우선이라 생각된다. 만약 순수 가우스 소거법으로 디코딩하고 있다면, 각 코드의 핵심이 가려지면서 필자처럼 멀리 돌아오는 길을 걸을 수도 있다. :)
디코딩 알고리즘
디코더 구현을 위해 관련 알고리즘을 살펴보았을 때 익숙하지 않은 이름들이 혼용되고 있어 접근이 쉽지 않았다. 그나마 조금이라도 익숙한 것이라면 가우스 소거법 정도지만, 아련한 선형대수의 기억만 가지고 있던 필자로서는 이마저도 부담이었다. 그 이름들을 나열해보면 다음과 같다.
| Belief Propagation(BP) | Hybrid | Maximum Likelihood(ML) |
|---|---|---|
| Sum Product, Greedy, Peeling | Inactivation Decoding(IDGE) | Gaussian Elimination(GE) |
| Luby Transform(LT) code | Raptor, RaptorQ code | |
다양한 이름에서 알 수 있는 것 처럼 논문에 따라, 서술하는 사람에 따라 다르게 불리우고 있지만 큰 맥락을 보면 신뢰성전파와 최대유사도 알고리즘으로 나눌 수 있을 것이다. 그리고 두 가지를 조합하여 디코딩 하는 알고리즘들이 있고 인액티베이션 디코더가 대표적이다.
루비트랜스폼 코드(이하 LT)가 최초의 실용적인 파운틴코드라 일컬어지는 것은 솔리톤분포에 의한 저밀도 매트릭스와 신뢰성전파(이하 BP) 디코딩 알고리즘의 조합에 그 핵심이 있다. 그럼 LT 코드를 가우스소거법(이하 GE)으로는 풀면 어떻게 될까. BP에 비해 더 적은 오버헤드만으로 복구할 수 있지만, 디코딩 복잡도가 크게 증가하게 된다.
그럼 BP로 풀 수 있는데까지 풀고 나머지를 GE로 해결하는 방법은 어떨까. 이 접근방법의 대표적인 예가 인액티베이션 디코딩이며, LT코드 매트릭스를 통째로 GE로 푸는 것에 비해 개선된 성능을 보이는 랩터(이하 R10)와 랩터Q(이하 RQ) 코드의 핵심이기도 하다.
프로그래머 입장에서는 R10과 RQ도 GE로 푸는 방법도 생각할 수 있지만, 저밀도 매트릭스에서 BP의 구현 용이성을 생각하면 BP를 통해 매트릭스 크기를 줄이고 최소한의 매트릭스만 GE로 푸는 것이 아무래도 합리적이다.
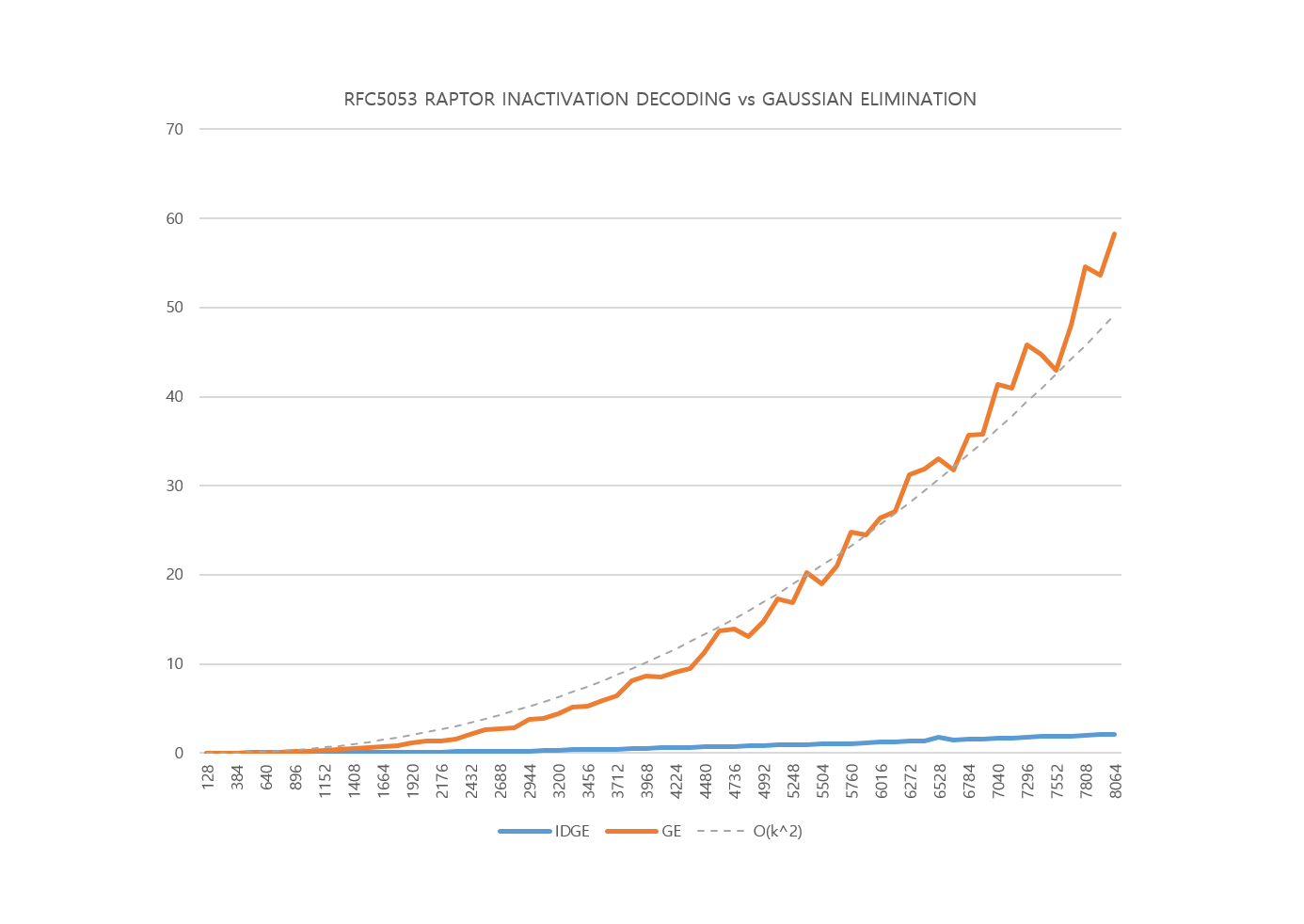
RFC 5053의 인액티베이션 디코딩을 실제 구현해 비교해 보면 거의 선형임을 볼 수 있지만 논문에서의 주장처럼 진짜 선형은 아직 달성해보지 못했다. 자료구조에 의해서도 많은 영향을 받기 때문에 어딘가 아직 핵심을 놓치고 있을 수도 있는 부분이라고 생각된다. 많은 응용논문에서 R10의 디코딩 복잡도가 심볼 수 K2에 비례하는 그래프를 보이고 있는데 이는 가우스 소거법을 사용하여 디코딩하기 때문인 것으로 보인다.
인코딩 알고리즘
Soliton Distribution
LT 인코딩 측면에서는 몇 개의 소스심볼과 XOR 되었는지를 나타내는 DEGREE 분포가 핵심이 된다. 여러가지 변형이 존재하지만 soliton가 그 중심에 있다.
TypeError: Cannot access offset of type string on string
An unforeseen error has occured. This is most likely a bug somewhere.
More info has been written to the DokuWiki error log.