This is an old revision of the document!
솔리톤 분포
Soliton Distribution
Ideal Soliton Distribution
Belief-Propagation 알고리즘으로 디코딩하는 것을 상정하여 디자인 된 Luby-Transform에 있어서 핵심이 되는 분포함수이다. BP 알고리즘은 Degree 1인 인코딩심볼로부터 디코딩을 시작하는데, Soliton Distribution은 BP에 적합한 Degree 분포를 생성한다.
Definition
| $\rho(1) = 1/k$ | |
| $\rho(i)=1/i(i − 1),$ | $(i = 2,…,k)$ |
Graph
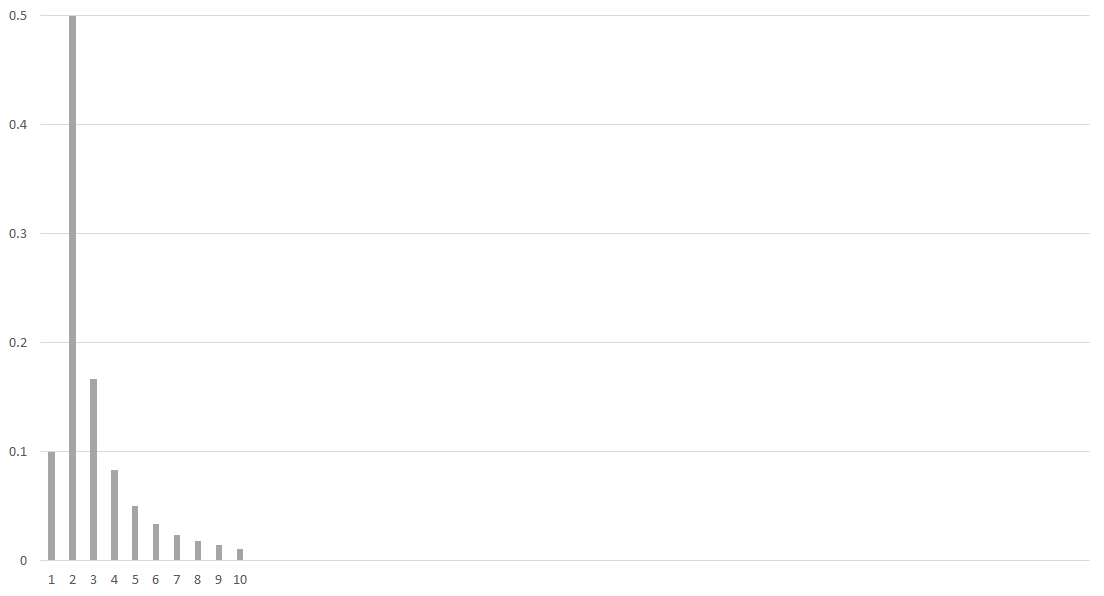 $$k = 10$$
$$k = 10$$
Soliton Distribution의 특징은 Degree 1과 2 사이에서 볼 수 있는 물결(ripple)에 있다. Degree 2 이후로는 함수의 정의에 따라 $1/i(i-1)$을 따라 줄어가는 형태를 가지지만, Degree 1은 일정수준 확보되는 것을 관찰할 수 있다.
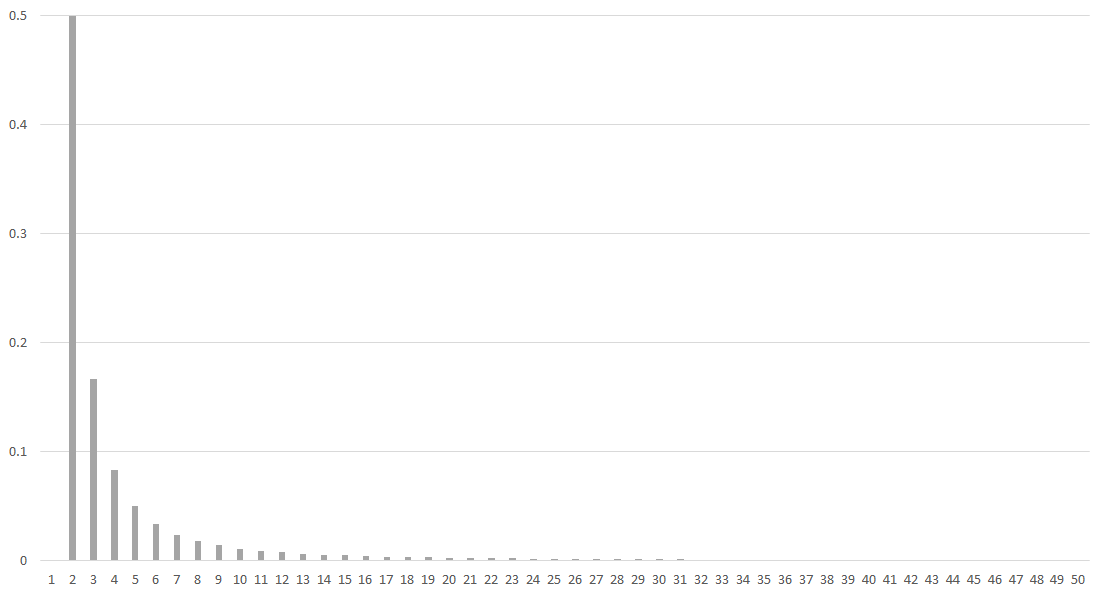 $$k = 10000$$
$$k = 10000$$
하지만 LT가 좋은 성능을 보이는 높은 k 값에서는 Degree 1의 비율이 극단적으로 감소하는 것이 보인다. 이 경우 BP 알고리즘은 충분한 수의 Degree 1인 인코딩 심볼을 확보하기 어려워져 결과적으로 디코딩에 더 많은 인코딩 심볼을 요구하게 된다.
Normalization
함수의 정의에 의해 $k\geq 1,\thinspace i\in\mathbb{N}$ 일 때, Probability Distribution의 조건 $\sum_i\rho(i)=1$ 을 만족한다. 따라서 별도의 normalization은 필요 없지만, 코드로 구현해보면 자료형의 정밀도 한계에 의해 누적합이 1의 근사치로 나타나기도 한다.
Reference
Math Symbols
| $P$ | $\rho$ | rho |
| $T$ | $\tau$ | tau |
| $M$ | $\mu$ | mu |
| $D$ | $\delta$ | delta |
Robust Soliton Distribution
Definition
| $\mu(i)=(\rho(i)+\tau(i)) / (\sum\rho(i)+\tau(i))$ |
Robust Soliton Distribution $\mu(i)$는 Ideal Soliton Distribution $\rho(i)$에 $\tau(i)$를 더하고 누적합이 1이 되도록 normalization을 수행한 것이다.
| $\tau(i)= 1/im,$ | $(i=1,2,\dots,m-1)$ |
| $\tau(i)= ln((k/m)/\delta)/m,$ | $(i=m)$ |
| $\tau(i)= 0,$ | $(i=m+1,\dots,k)$ |
$\tau(i)$의 정의는 논문보다는 $k/R$을 m으로 표기하는 위키피디아의 표기방법이 더 직관적인 것으로 생각되어 이를 따랐다. 논문에서 정의하는 $R$은 상수 $c$와 $\delta$에 의해 그 값이 결정되는데, 최종적으로는 자연수 m으로 표현되기 때문이다.
Graph
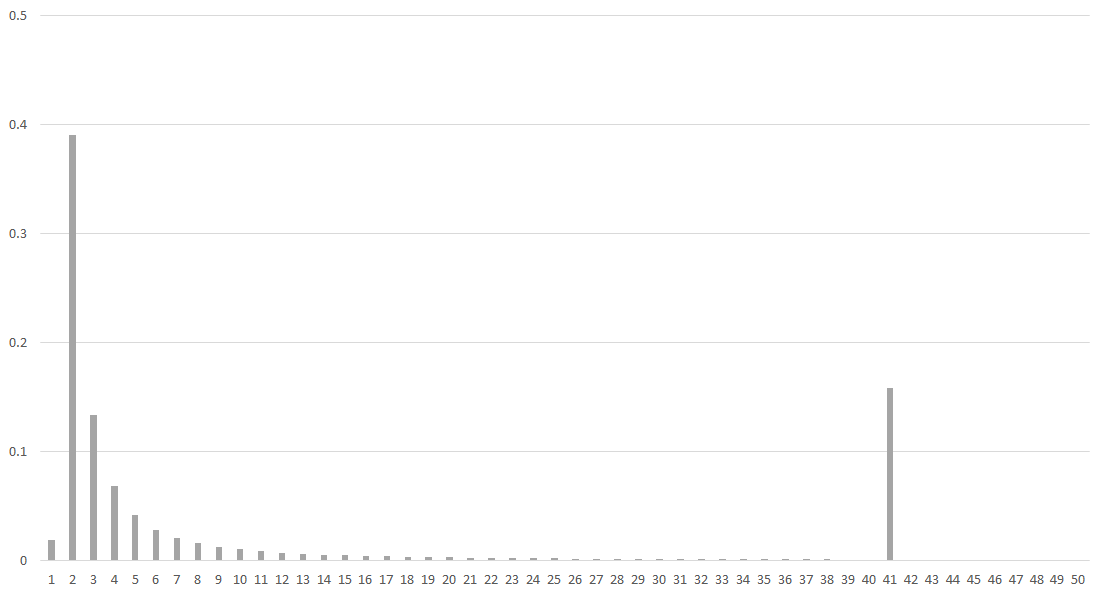 $$k = 10000, c = 0.2, \delta = 0.05 ( S = 244, M = 41, Z = 1.31 )$$
$$k = 10000, c = 0.2, \delta = 0.05 ( S = 244, M = 41, Z = 1.31 )$$
CDF
gofountain하다 보면 솔리톤분포 생성함수를 CDF(Cumulative Distribution Function, 누적분포함수)라고 지칭하고 있는데 PDF와의 차이점을 공부하다가 정리해본다. 우선 용어에서 혼란이 있었는데 정리하자면 하기와 같다.
| Probability Distribution Function | Probability Mass Function | Discrete variable |
| Probability Density Function | Continuous variable | |
| Cumulative Distribution Function | PMF의 누적합 또는 PDF의 적분 |
먼저 CDF의 정의를 찾아보자. A real-valued random variable X 대한 함수의 정의는, $$F(x) = P(X\leq x)$$ 이 때, P는 임의의 실수 X가 x보다 작거나 같을 확률이다. Continuous random variables 에서는 PDF(Probability Density Function)에 대한 적분이고, $$F(x)=\int_{-\infty}^x f(t)dt$$ Discrete random variables 에서는 PMF(Probability Mass Function)에 대한 누적합이다. $$F(x)=\sum\limits_{t \leq x} f(t)$$
Go implementation
Ideal Soliton Distribution
Reference
하기 CDF는 gofountain에서 발췌하였다. 한 개의 파라메터 n 을 가지는데, 관련 논문에서는 통상 소스심볼의 수 k로 표기하며 여기서는 위키피디아의 표기 N을 참조한 것으로 생각된다. 이 값은 최대 degree로도 해석할 수 있으며, 따라서 소스심볼의 수 k를 넘을 수 없다.
package main import( "fmt" ) func SolitonDistribution(n int) []float64 { cdf := make([]float64, n+1) cdf[1] = 1 / float64(n) for i := 2; i < len(cdf); i++ { cdf[i] = cdf[i-1] + (1 / (float64(i) * float64(i-1))) } return cdf } func main() { for i:=1;i<20;i++{ fmt.Println(SolitonDistribution(i)) } }
MacBook-Pro-Retina:gofountain-LT-experiment gomida$ go run soliton.go [0 1] [0 0.5 1] [0 0.3333333333333333 0.8333333333333333 0.9999999999999999] [0 0.25 0.75 0.9166666666666666 1] [0 0.2 0.7 0.8666666666666666 0.95 1] [0 0.16666666666666666 0.6666666666666666 0.8333333333333333 0.9166666666666666 0.9666666666666667 1] [0 0.14285714285714285 0.6428571428571428 0.8095238095238094 0.8928571428571428 0.9428571428571428 0.9761904761904762 1] [0 0.125 0.625 0.7916666666666666 0.875 0.925 0.9583333333333334 0.9821428571428572 1] [0 0.1111111111111111 0.6111111111111112 0.7777777777777778 0.8611111111111112 0.9111111111111112 0.9444444444444445 0.9682539682539684 0.9861111111111113 1.0000000000000002] [0 0.1 0.6 0.7666666666666666 0.85 0.9 0.9333333333333333 0.9571428571428572 0.9750000000000001 0.9888888888888889 1] [0 0.09090909090909091 0.5909090909090909 0.7575757575757576 0.8409090909090909 0.890909090909091 0.9242424242424243 0.9480519480519481 0.965909090909091 0.9797979797979799 0.990909090909091 1] [0 0.08333333333333333 0.5833333333333334 0.75 0.8333333333333334 0.8833333333333334 0.9166666666666667 0.9404761904761906 0.9583333333333335 0.9722222222222223 0.9833333333333334 0.9924242424242424 1] [0 0.07692307692307693 0.5769230769230769 0.7435897435897435 0.8269230769230769 0.8769230769230769 0.9102564102564102 0.9340659340659341 0.951923076923077 0.9658119658119658 0.9769230769230769 0.9860139860139859 0.9935897435897435 0.9999999999999999] [0 0.07142857142857142 0.5714285714285714 0.738095238095238 0.8214285714285714 0.8714285714285714 0.9047619047619048 0.9285714285714286 0.9464285714285715 0.9603174603174603 0.9714285714285714 0.9805194805194805 0.988095238095238 0.9945054945054944 0.9999999999999999] [0 0.06666666666666667 0.5666666666666667 0.7333333333333333 0.8166666666666667 0.8666666666666667 0.9 0.9238095238095239 0.9416666666666668 0.9555555555555556 0.9666666666666667 0.9757575757575757 0.9833333333333333 0.9897435897435897 0.9952380952380951 0.9999999999999999] [0 0.0625 0.5625 0.7291666666666666 0.8125 0.8625 0.8958333333333334 0.9196428571428572 0.9375000000000001 0.951388888888889 0.9625 0.9715909090909091 0.9791666666666666 0.985576923076923 0.9910714285714285 0.9958333333333332 0.9999999999999999] [0 0.058823529411764705 0.5588235294117647 0.7254901960784313 0.8088235294117647 0.8588235294117648 0.8921568627450981 0.9159663865546219 0.9338235294117648 0.9477124183006537 0.9588235294117647 0.9679144385026738 0.9754901960784313 0.9819004524886877 0.9873949579831932 0.992156862745098 0.9963235294117646 0.9999999999999999] [0 0.05555555555555555 0.5555555555555556 0.7222222222222222 0.8055555555555556 0.8555555555555556 0.888888888888889 0.9126984126984128 0.9305555555555557 0.9444444444444445 0.9555555555555556 0.9646464646464646 0.9722222222222222 0.9786324786324786 0.9841269841269841 0.9888888888888888 0.9930555555555555 0.9967320261437908 0.9999999999999999] [0 0.05263157894736842 0.5526315789473684 0.719298245614035 0.8026315789473684 0.8526315789473684 0.8859649122807017 0.9097744360902256 0.9276315789473685 0.9415204678362573 0.9526315789473684 0.9617224880382774 0.969298245614035 0.9757085020242914 0.9812030075187969 0.9859649122807016 0.9901315789473683 0.9938080495356035 0.9970760233918127 0.9999999999999998] MacBook-Pro-Retina:gofountain-LT-experiment gomida$
각 라인의 마지막 값을 살펴보면 누적 합이 1이 아닌 경우들을 관찰 할 수 있다. 이는 분수를 float 자료형으로 풀어 계산 후 합산했기 때문으로 수학적으로는 1이 되어야 한다.
Go implementation
Robust Soliton Distribution
Reference
하기 CDF 역시 gofountain에서 발췌하였다. 세 개의 파라메터 n, m, delta를 가지는데, 원본 논문의 수식에 대입하면 각각 $k, k/R, \delta$에 해당한다.
package main import( "fmt" "math" ) func robustSolitonDistribution(n int, m int, delta float64) []float64 { pdf := make([]float64, n+1) pdf[1] = 1/float64(n) + 1/float64(m) total := pdf[1] for i := 2; i < len(pdf); i++ { pdf[i] = (1 / (float64(i) * float64(i-1))) if i < m { pdf[i] += 1 / (float64(i) * float64(m)) } if i == m { pdf[i] += math.Log(float64(n)/(float64(m)*delta)) / float64(m) } total += pdf[i] } cdf := make([]float64, n+1) for i := 1; i < len(pdf); i++ { pdf[i] /= total cdf[i] = cdf[i-1] + pdf[i] } return cdf } func main() { for i:=1;i<20;i++{ fmt.Println(robustSolitonDistribution(10, i, 0.01)) } }
[0 0.55 0.8 0.8833333333333334 0.925 0.9500000000000001 0.9666666666666668 0.9785714285714286 0.9875 0.9944444444444445 1] [0 0.1302280017970026 0.9131813321353315 0.9493557770789434 0.9674429995507493 0.9782953330338329 0.9855302220225552 0.9906979998716426 0.9945738332584582 0.9975883703370925 0.9999999999999999] [0 0.12610165570711526 0.320104202948831 0.9320991084653996 0.9563494268706141 0.9708996179137428 0.9805997452758286 0.9875284076773184 0.9927249044784358 0.9967666242126382 1] [0 0.12329593729561326 0.34346725389492266 0.4315357805346464 0.9471588840161658 0.9647725893441105 0.9765150595627403 0.984902538290333 0.9911931473360276 0.9960858432604567 1] [0 0.121147013137301 0.363441039411903 0.4576664940742482 0.5115096110241597 0.9596176622875665 0.9730784415250444 0.9826932838375286 0.9899044155718918 0.9955130735875076 1.0000000000000002] [0 0.11940896315883283 0.3806160700687796 0.48012353936780694 0.5360964908485099 0.5734117918356452 0.9701477592102921 0.9808092737780449 0.9888054097038597 0.9950246265350489 1.0000000000000002] [0 0.11795852541253558 0.39550799697144284 0.49958904880603305 0.5574118553808054 0.5955749077201551 0.6233298548760459 0.9791837896330822 0.987857210619298 0.9946032047196881 1.0000000000000002] [0 0.11672265445912686 0.408529290606944 0.5166058225135429 0.5760479150621723 0.6149554665485479 0.6430553648442636 0.6646706712255834 0.987030816171208 0.9942359182983146 0.9999999999999999] [0 0.11565346630380048 0.42000469341906493 0.5316001433613285 0.5924703887843814 0.6320360483093658 0.6604421628401238 0.6821815362054998 0.6995730348978006 0.9939129754576947 1] [0 0.1147174554617686 0.43019045798163225 0.5449079134434008 0.6070465351518588 0.6471976445634778 0.67587700842892 0.6977279523263997 0.7151404232447038 0.7294801051774249 1] [0 0.15076493547192388 0.5815218939631349 0.7370730178627389 0.820831315347141 0.8746759351585425 0.9129654425799835 0.9420244437480414 0.9651007093814992 0.9840460385743997 1] [0 0.1473645038675208 0.5827596289306505 0.7390553148507483 0.8227851465936578 0.8763722389091199 0.9143297626325722 0.9430371335158554 0.965763802131788 0.9843704314079902 1] [0 0.1443910216486884 0.5838419571012182 0.740788719762836 0.8244936598490322 0.8778555591539823 0.9155227821927705 0.9439226725791585 0.9663436386736753 0.9846540943175307 1] [0 0.14176882867255808 0.5847964182743022 0.7423173390215889 0.826000328168585 0.8791636389207943 0.916574857598275 0.9447035934460047 0.9668549729260919 0.9849042450950518 1.0000000000000002] [0 0.1394391447732454 0.5856444080476306 0.7436754387906421 0.8273389256545893 0.8803258006684226 0.9175095726079547 0.9453974015626038 0.967309267169828 0.9851264912241872 1] [0 0.13735561099348023 0.5864028007798578 0.7448900442338735 0.8285360893901595 0.8813651705414981 0.9183455273474351 0.9460179031886125 0.9677155615186265 0.9853252552357393 1] [0 0.1354811732143924 0.5870850839290338 0.7459827562175187 0.8296131100535634 0.8823002329702716 0.9190975886581313 0.9465761334899745 0.9680810816192431 0.9855040720017524 1.0000000000000002] [0 0.13378585919872585 0.5877021671944028 0.746971047192886 0.8305872091920896 0.883145939591589 0.9197777819912402 0.9470810185624087 0.9684116721336341 0.9856658008001364 0.9999999999999999] [0 0.1322451638587793 0.588262970268363 0.7478692025117174 0.8314724670201411 0.8839145147572433 0.92039593927001 0.9475398563181995 0.9687121116157873 0.9858127793561466 1.0000000000000004]
Python implementation
Soliton Distribution
Reference
from __future__ import print_function, division import random from math import ceil def soliton(N, seed): prng = random.Random() prng.seed(seed) while 1: x = random.random() # Uniform values in [0, 1) i = int(ceil(1/x)) # Modified soliton distribution yield i if i <= N else 1 # Correct extreme values to 1 if __name__ == '__main__': N = 10 T = 10 ** 5 # Number of trials s = soliton(N, random.randint(0, 2 ** 32 - 1)) f = [0]*N for j in range(T): i = next(s) f[i-1] += 1 print("k\tFreq.\tExpected Prob\tObserved Prob\n"); print("{:d}\t{:d}\t{:f}\t{:f}".format(1, f[0], 1/N, f[0]/T)) for k in range(2, N+1): print("{:d}\t{:d}\t{:f}\t{:f}".format(k, f[k-1], 1/(k*(k-1)), f[k-1]/T))
MacBook-Pro-Retina:work gomida$ python soliton.py k Freq. Expected Prob Observed Prob 1 10148 0.100000 0.101480 2 49794 0.500000 0.497940 3 16661 0.166667 0.166610 4 8335 0.083333 0.083350 5 5031 0.050000 0.050310 6 3306 0.033333 0.033060 7 2469 0.023810 0.024690 8 1771 0.017857 0.017710 9 1419 0.013889 0.014190 10 1066 0.011111 0.010660 MacBook-Pro-Retina:work gomida$
TypeError: Cannot access offset of type string on string
An unforeseen error has occured. This is most likely a bug somewhere.
More info has been written to the DokuWiki error log.